Q. The radius of the circle $ x^{2}+y^{2}+z^{2}-2y-4z-11=0 $ , $ x+2y+2z-15=0 $ is:
Jharkhand CECEJharkhand CECE 2005
Solution:
Radius of a circle in a sphere
$ =\sqrt{\text{Radius of sphere})^2 - (\bot \text{distance from origin to sphere})^2}$
Given equation of sphere is
$ x^{2}+y^{2}+z^{2}-2y-4z-11=0 $
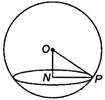
Whose centre is $ O(0, 1, 2) $ and radius $ OP $ is $ 4 $ .
$ \therefore $ Distance of a plane $ x+2y+2z-15=0 $
from $ (0, 1, 2) $ is
$ ON=\frac{|0+2+4-15|}{\sqrt{1+4+4}} =\frac{9}{3}=3 $
In $ \Delta ONP $ , $ OP^{2}=ON^{2}+NP^{2} $
$ \Rightarrow $ $ NP^{2}=(4)^{2}-(3)^{2}=7 $
$ \Rightarrow $ $ NP=\sqrt{7} $