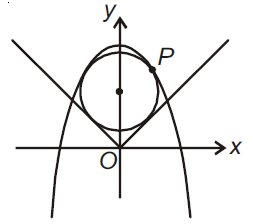
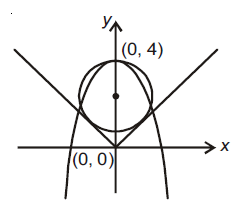
Q. The radius of a circle, having minimum area, which touches the curve $y = 4 - x^2$ and the lines, $ y = | x |$ is :
Solution:
$x^2 = -(y - 4)$
Let a point on the parabola $P\left(\frac{t}{2},4-\frac{t^{2}}{4}\right)$
Equation of normal at P is
$y+\frac{t^{2}}{4}-4=\frac{1}{t}\left(x-\frac{t}{2}\right)$
$\Rightarrow x-ty-\frac{t^{3}}{4}+\frac{7}{2}t=0$
It passes through centre of circle, say (0, k)
$-tk-\frac{t^{3}}{4}+\frac{7}{2}t=0 ...\left(i\right)$
$t=0, t^{2}=14-4k$
Radius$=r=\left|\frac{0-k}{\sqrt{2}}\right|$ (Length of perpendicular from (0, k) to y = x)
$\Rightarrow r=\frac{k}{\sqrt{2}}$
Equation of circle is $x^{2}+\left(y-k\right)^{2}=\frac{k^{2}}{2}$
It passes through point P
$\frac{t^{2}}{4}+\left(4-\frac{t^{2}}{4}-k\right)^{^2}=\frac{k^{2}}{2}$
$t^{4} + t^{2} \left(8k - 28\right) + 8k^{2}-128k + 256 = 0 ...\left(ii\right)$
For t = $0 \Rightarrow k^{2}-16k+32=0$
$k=8\pm4\sqrt{2}$
$\therefore r=\frac{k}{\sqrt{2}}=4(\sqrt{2}-1)$
(discarding $4(\sqrt{2}+1)) \ldots$ (iii)
For $t =\pm \sqrt{14-4k}$
$\left(14-4k\right)^{2}+\left(14-4k\right)\left(8k-28\right)+8k^{2}-128k+256=0$
$2k^{2}+4k-15=0$
$k=\frac{-2\pm\sqrt{34}}{2}$
$\therefore r=\frac{k}{\sqrt{2}}=\frac{\sqrt{17}-\sqrt{2}}{2}$ (Ignoring negative ...(iv) value of r)
From (iii) & (iv),
$r_{min}=\frac{\sqrt{17}-\sqrt{2}}{2}$
But from options, $r=4\left(\sqrt{2}-1\right)$