Q.
The potential energy of a particle executing $SHM$ is given by $V ( x )=\frac{1}{2} \,kx ^{2}$ where $k$ is
force constant. For $k =0.5 \,N / m$ the graph of $PE$ as a function of $x$ is shown below. Find
the position of particle having total energy $1 \,J$ moving in this potential at which it must
turn back to its original position.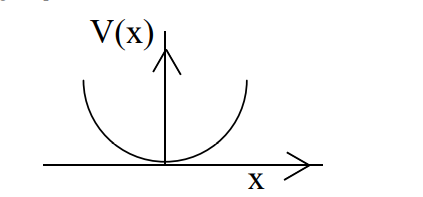
Solution: