Question

The potential energy function for a particle executing linear $SHM$ is given by $V(x) = \frac{1}{2}kx^2$ where $k$ is the force constant of the oscillator. For $k = 0.5\, Nm^{-1}$, the graph of $V(x)$ versus x is shown in the figure. A particle of total energy $E$ turns back when it reaches $x = ± x_m$. If $V$ and $K$ indicate the potential energy and kinetic energy, respectively of the particle at $x = +x_m$, then which of the following is correct?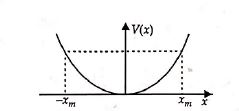

• A. $V=0$, $K = E$
• B. $V=E$, $K = 0$
• C. $V < E$, $K = 0$
• D. $V=0$, $K < E$

Answer 1

Answer: (B)

At any instant, the total energy of an oscillator is the sum of kinetic energy and potential energy.
Total energy, $E = K + V$
$E = \frac{1}{2}\,mv^{2} + \frac{1}{2} kx^{2}$
At $x = +x_{m}$, the particle turns back, therefore its velocity at this point is zero, i.e. $v = 0$
$\therefore K = 0$
$\therefore E = \frac{1}{2}kx^{2} = V$