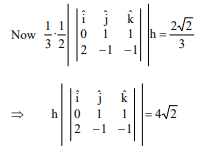Question

The position vectors of the vertices $A , B$ and $C$ of a tetrahedron are $(1,1,1),(1,0,0)$ and (3, $0,0)$ respectively. The altitude from the vertex $D$ to the opposite face $A B C$ meets the median line through $A$ of the $\triangle ABC$ at a point $E$. If the length of side $AD$ is 4 and volume of the tetrahedron is $\frac{2 \sqrt{2}}{3}$ then the correct statement(s) is/are

• A. The altitude from the vertex $D$ is 2 .
• B. There is exactly one position for the point $E$.
• C. There can be two positions for the point $E$.
• D. Vector $\hat{ j }-\hat{ k }$ is normal to the plane $ABC$.

Answer 1

Answer: (A), (C), (D)

Given $V=\frac{2 \sqrt{2}}{3}$


$\left[\right.$ Note $ABC$ is a right triangle $\rightarrow$ Area $\left.=\frac{1}{2}(2)(\sqrt{2})=\sqrt{2}\right]$
$h |\hat{ i }(-1+1)+2(\hat{ j }-\hat{ k })|=4 \sqrt{2}$
$\Rightarrow h |\hat{ j }-\hat{ k }|=2 \sqrt{2} \Rightarrow h =2 \Rightarrow \text { A and } D$
Let $E$ divides $AM$ in the ratio $\lambda: 1$
hence $E:\left(\frac{2 \lambda+1}{\lambda+1}, \frac{1}{\lambda+1}, \frac{1}{\lambda+1}\right)$
Now, $( AE )^2+( DE )^2=( AD )^2$
$\left(\frac{2 \lambda+1}{\lambda+1}-1\right)^2+\left(1-\frac{1}{\lambda+1}\right)^2+\left(1-\frac{1}{\lambda+1}\right)^2+4=16 $
$\left(\frac{\lambda}{\lambda+1}\right)^2+2\left(\frac{\lambda}{\lambda+1}\right)^2=12 \Rightarrow\left(\frac{\lambda}{\lambda+1}\right)^2=4 \Rightarrow \frac{\lambda}{\lambda+1}=2 \text { or }-2$
$\therefore $ These are two positions for $E$ which are $(-1,3,3)$ and $(3,-1,-1)$