Q.
The position vector of the centre of mass $\left( r _{ cm }\right)$ of an asymmetric uniform bar of negligible area of cross-section as shown figure is $(aL, bL)$. Find $\frac{ a }{ b }$.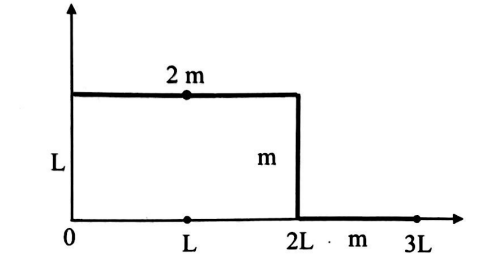
System of Particles and Rotational Motion
Solution:
