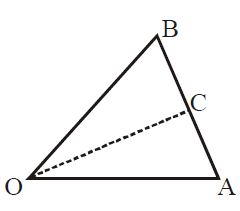
Q.
The position vector of $A$ and $B$ are $ 2\hat{i}+2\hat{j}+\hat{k}$ and $2\hat{i}+4\hat{j}+4\hat{k}$
The length of the internal bisector of $\angle BOA$ triangle $AOB$ is
VITEEEVITEEE 2019
Solution:
We have,
$OA=\left|2\hat{i}+2\hat{j}+\hat{k}\right|=3 ;OB=\left|2\hat{i}+4\hat{j}+4\hat{k}\right|=6$
Since the internal bisector divides opposite side in the
ratio of adjacent sides
$\therefore \frac{AC}{BC}=\frac{3}{6}=\frac{1}{2}$
where $OC$ is the bisector of $\angle BOA .$
$\therefore $ Position vector of $C$ is
$\frac{2\left(2\hat{i}+2\hat{j}+\hat{k}\right)+\left(2\hat{i}+4\hat{j}+4\hat{k}\right)}{2+1}=2\hat{i}+\frac{8}{3} \hat{j}+2\hat{k}$
$\therefore OC=\left|2\hat{i}+\frac{8}{3} \hat{j}+2\hat{k}\right|=\sqrt{\frac{136}{9}}$