Q.
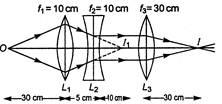
The position of final image formed by the given lens combination from the third lens will be at a distance of [ $ {{f}_{1}}=+10\text{ }cm, $ $ {{f}_{2}}=-10cm, $ $ {{f}_{3}}=+30\text{ }cm $ ]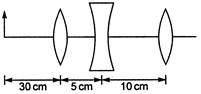
Solution:
For first lens, $ {{u}_{1}}=-30\,cm,{{f}_{1}}=10\,cm $
$ \frac{1}{f}=\frac{1}{v}-\frac{1}{u} $ or $ \frac{1}{v}=\frac{1}{f}+\frac{1}{u} $
Or $ \frac{1}{v}=\frac{1}{10}-\frac{1}{30}=\frac{1}{15} $
Or $ v=15\text{ }cm $
Therefore, image formed by convex lens $ ({{L}_{1}}) $ is at point $ {{I}_{1}} $ and acts as virtual object for concave lens $ ({{L}_{2}}) $ .
The image $ {{I}_{1}} $ is formed at focus of concave lens (as shown) and so emergent rays will be parallel to the principal axis. For lens $ {{L}_{2}} $
$ {{u}_{2}}=15-5=10\,cm,{{f}_{2}}=-10\,cm. $
These parallel rays are incident on the third convex lens $ ({{L}_{3}}) $ and will be brought to convergence at the focus of the lens 1, 3. Hence, distance of final image from third lens $ {{L}_{3}}, $ $ {{v}_{2}}={{f}_{3}}=30cm $