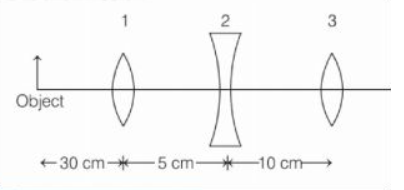
Q.
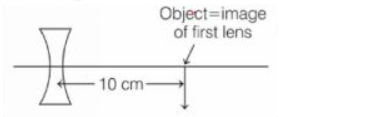
The position of final image formed by the given lens combination from the third lens will be at a distance of $\left(f_{1}=+10, f_{2}=-10\, cm\right.$ and $\left.f_{3}=+30\, cm \right)$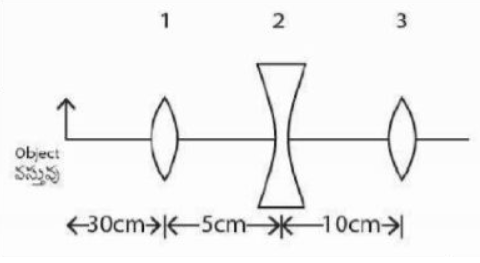
TS EAMCET 2020
Solution: