Q.
The position of a wave (of wavelength $\lambda$ ).
$y(x, t)=A \sin 2 \pi\left(\frac{x}{\lambda}-3750 t\right)$
is shown at $t=0$, find $x$-coordinate of point $P$ in metres, if the wave speed is $300\, m / sec$ :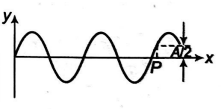
Waves
Solution: