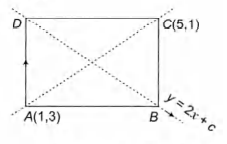
Question

The points $(1, 3)$ and $(5, 1)$ are two opposite vertices of a rectangle. The other two vertices lie on the line $y = 2x + c$. Find c and the remaining vertices.

Answer 1

Since, diagonals of rectangle bisect each other, so mid point of $(1, 3)$ and $(5, 1)$ must satisfy $y = 2x+ c$, i.e. $(3, 2)$ lies on it.

$\Rightarrow 2=6+c \Rightarrow c=-4$
$\therefore $ Other two vertices lies on $y = 2x - 4$
Let the coordinate of $B$ be $(x, 2x - 4)$.
$\therefore $ Slope of $AB$ . Slope of $BC = - 1 $
$\Rightarrow \Bigg(\frac{2 x - 4 - 3 }{x-1}\Bigg).\Bigg(\frac{2 x - 4 - 1}{x-5}\Bigg)=-1$
$\Rightarrow (x^2 - 6x + 8) = 0$
$\Rightarrow x = 4,2$
$\Rightarrow y =4,0$
Hence, required points are $(4, 4), (2, 0)$.