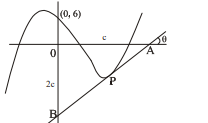
Question

The point(s) at each of which the tangents to the curve $y=x^3-3 x^2-7 x+6$ cut off on the positive semi axis OX a line segment half that on the negative semi axis OY then the co-ordinates the point(s) is/ are given by:

• A. $(-1,9)$
• B. $(3,-15)$
• C. $(1,-3)$
• D. none

Answer 1

Answer: (B)

If $OA = a ; OB =2 a \Rightarrow \tan \theta=2$
slope of the tangent is 2
$\Rightarrow\left(\frac{d y}{d x}\right)_{x_1 y_1}=2 \Rightarrow 3 x_1^2-6 x_1-7=2 \Rightarrow 3 x_1^2-2 x_1-3=0 $
$\Rightarrow x_1=3 \text { or }-1 \text { (rejected) }$
$\Rightarrow(3,-15) \Rightarrow B]$
[Also for the point $P ; x \& y$ both positive or $x$ positive \& $y$ negative or $x \& y$ both negative ]