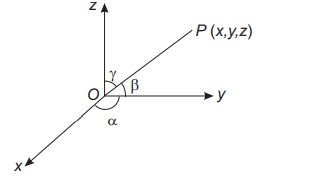
Question

The point $P(x, y, z)$ lies in the first octant and its distance from the origin is $12$ units. If the position vector of $P$ makes $45^\circ$ and $60^\circ$ with the $x-axis$ and $y-axis$ respectively, then the co-ordinates of $P$ are

• A. $\left(3\sqrt{3},6, 3\sqrt{2}\right)$
• B. $\left(4\sqrt{3},8, 4\sqrt{2}\right)$
• C. $\left(6\sqrt{2},6, 6\right)$
• D. $\left(6,6, 6\sqrt{2}\right)$
• E. $\left(4\sqrt{2},8, 4\sqrt{3}\right)$

Answer 1

Answer: (C)

Given, $O P=12$ units
and $\alpha=45^{\circ}$ and $\beta=60^{\circ}$

Let direction cosines of line $OP$ is $<\,l, m, n>\,$
$\therefore \, l^{2}+m^{2}+n^{2}=1$
$\Rightarrow \, \cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=1$
$\Rightarrow \,\cos ^{2} 45^{\circ}+\cos ^{2} 60^{\circ}+\cos ^{2} \gamma=1$
$\Rightarrow \, \left(\frac{1}{\sqrt{2}}\right)^{2}+\left(\frac{1}{2}\right)^{2}=1-\cos ^{2} \gamma$
$\Rightarrow \, \sin ^{2} \gamma=\frac{1}{2}+\frac{1}{4}=\frac{3}{4}$
$\Rightarrow \,\sin \gamma=\frac{\sqrt{3}}{2}=\sin 60^{\circ}$
$\therefore \, \gamma=60^{\circ}$
So, the coordinates of $P \equiv(I \cdot O P, m \cdot O P, n \cdot O P)$
$\equiv(O P \cos \alpha, O P \cos \beta, O P \cos \gamma) $
$\equiv\left(12 \cdot \frac{1}{\sqrt{2}}, 12 \cdot \frac{1}{2}, 12 \cdot \frac{1}{2}\right) $
$\equiv(6 \sqrt{2}, 6,6)$