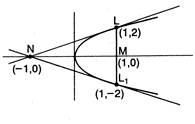
Q. The point of intersection of tangents at the ends of the latus-rectum of the parabola $ {{x}^{2}}+{{y}^{2}}-18x+16y+120=0 $ is equal to :
JamiaJamia 2004
Solution:
Equation to the tangent at $ ({{x}_{1}}{{y}_{1}}) $ on the parabola $ {{y}^{2}}=4ax $ is $ y{{y}_{1}}=2a(x+{{x}_{1}}) $ $ \therefore $ In this case, $ a=1 $ The co-ordinates at the ends of the latus rectum of the parabola $ {{y}^{2}}=4x $ are L (1, 2) and $ {{L}_{1}}(1,-2) $ Equation of tangent at L and $ {{L}_{1}} $ are $ 2y=(2x+1) $ and $ -2y=2(x+1) $ which gives $ x=-1,\text{ }y=0 $
thus the required point of intersection is $ (-1,0) $