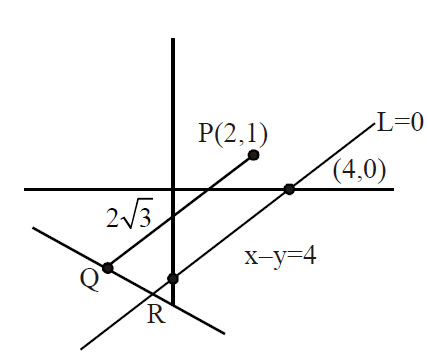
Q. The point $(2, 1)$ is translated parallel to the line $L : x-y = 4$ by $2\sqrt{3}$ units. If the new point $Q$ lies in the third quadrant, then the equation of the line passing through $Q$ and perpendicular to $L$ is :
Solution:
$x-y=4$
To find equation of R
slope of L = 0 is 1
$\Rightarrow $ slope of QR = - 1
Let QR is y = mx + c
$y=-x+c$
$x+y-c=0$
distance of QR from (2,1) is $2\sqrt{3}$
$2\sqrt{3}=\frac{\left|2+1-c\right|}{\sqrt{2}}$
$2\sqrt{6}=\left|3-c\right|$
$c-3=\pm2\sqrt{6}\,c=3\pm2\sqrt{6}$
Line can $be x+y=3\pm2\sqrt{6}$
$x+y=3-2\sqrt{6}$