Question

The number of distinct solutions of the equation, $log_{\frac{1}{2}}\left|sin\,x\right| = 2 - log_{\frac{1}{2}}\left|cos\,x\right|$ in the interval $\left[0, 2\pi \right]$, is__________.

Answer 1

$log_{1/2}\left|sin\,x\right|=2-log_{1/2}\left|cos\,x\right|;\,x\,\in\left[0, 2\pi\right]$
$\Rightarrow log_{1/2}\left|sin\,x\right|+ log_{1/2}\left|cos\,x\right|=2$
$\Rightarrow log_{1/2}\left|sin\,x\,cos\,x\right|=2$
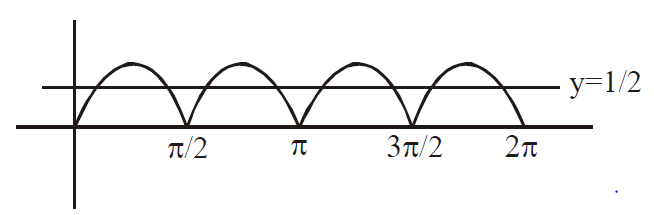
$\left|sinxcosx\right|=\frac{1}{4} \Rightarrow \left|sin2x\right|=\frac{1}{2}$
$\Rightarrow 8$ solutions