Question

The nearest point on the line $3x + 4y = 12$ from the origin is

• A. $\left(\frac{36}{25} , \frac{48}{25}\right) $
• B. $\left(3 , \frac{3}{4}\right) $
• C. $\left(2 , \frac{3}{2}\right) $
• D. None of these

Answer 1

Answer: (A)

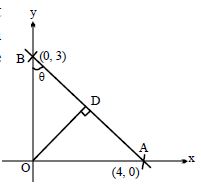
If ‘$D$’ be the foot of altitude, drawn from origin to the given line, then ‘$D$’ is the required point.
Let $\angle OBA = \theta$
$\Rightarrow \, \tan \theta = 4/3$
$\Rightarrow \, \angle DOA = \theta $
we have $OD = 12/5$
If $D$ is $(h, k)$ then $h = OD \cos \theta, k = OD \sin \theta$
$\Rightarrow \, h = 36/25, k = 48/25$.