Q.
The monochromatic beam of light is incident at $60^{\circ}$ on one face of an equilateral prism of refractive index $n$ and emerges from the opposite face making an angle $\theta(n)$ with the normal (see the figure). For $n = \sqrt{3}$ the value of $\theta$ is $60^{\circ}$ and $\frac{d\theta}{dn} = m$. The value of $m$ is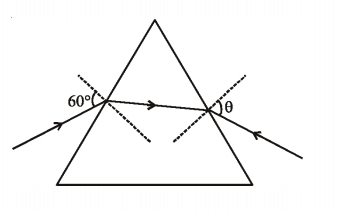
Ray Optics and Optical Instruments
Solution:
