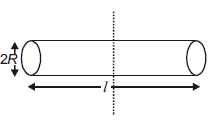
Q. The moment of inertia of a uniform cylinder of length $l$ and radius $R$ about its perpendicular bisector is $l$. What is the ratio $\frac{l}{R}$ such that the moment of inertia is minimum ?
Solution:
$I = \frac{mR^{2}}{4} + \frac{m l^{2}}{12}$
$I = \frac{m}{4} \left[R^{2} + \frac{l^{2}}{3}\right] $
$= \frac{m}{4} \left[\frac{v}{\pi l} + \frac{l^{2}}{3}\right] $
$\frac{dl}{d l} = \frac{m}{4} \left[ \frac{-v}{\pi l^{2}} + \frac{2 l}{3}\right] = 0$
$\frac{v}{\pi l^{2} } = \frac{2 l}{3} $
$v= \frac{2\pi l^{3}}{3}$
$\pi R^{2} l = \frac{2 \pi l^{3}}{3} $
$\frac{l^{2}}{R^{2}} = \frac{3}{2}$
$\frac{l}{R} = \sqrt{\frac{3}{2}}$