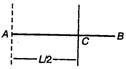
Q. The moment of inertia of a straight thin rod of mass $M$ and length $L$ about an axis perpendicular to its length and passing through its one end, is
Rajasthan PETRajasthan PET 2004
Solution:
From theorem of parallel axis
$ {{I}_{A}}={{I}_{C}}+M{{\left( \frac{L}{2} \right)}^{2}} $
$ =\frac{M{{L}^{2}}}{12}+\frac{M{{L}^{2}}}{4} $
$ {{I}_{A}}=\frac{M{{L}^{2}}}{3} $