Q.
The moment of inertia of a solid flywheel about its axis is $0.1 \,kg\, m^2$. A tangential force of 2 kg wt. is applied round the circumference of the flywheel with the help of a string and mass arrangement as shown in the figure. If the radius of the wheel is 0.1 m, find the acceleration of the mass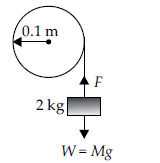
System of Particles and Rotational Motion
Solution: