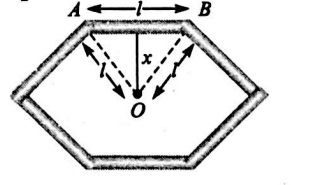
Q. The moment of inertia of a rod of length $l$ about an axis passing through its centre of mass and perpendicular to rod is $I$. The moment of inertia of hexagonal shape formed by six such rods, about an axis passing through its centre of mass and perpendicular to its plane will be
System of Particles and Rotational Motion
Solution:
Moment of inertia of rod $A B$ about its centre and perpendicular to the length $=\frac{m l^{2}}{12}=I$
$ \Rightarrow m l^{2}=12 I$
Now moment of inertia of the rod about the axis which is passing through $O$ and perpendicular to the plane of hexagon $I_{\text{ rod }}=\frac{m l^{2}}{12}+m x^{2}$
[From the theorem of parallel axes]
$=\frac{m l^{2}}{12}+m\left(\frac{\sqrt{3}}{2} l\right)^{2}=\frac{5 m l^{2}}{6}$
Now the moment of inertia of system,
$I_{\text {system }}=6 \times I_{\text {rod }}=6 \times \frac{5 m l^{2}}{6}=5 m l^{2} $
$I_{\text {system }}=5(12 I)=60 I$ $\left[\right.$ As $\left.m l^{2}=12 I\right]$