Q. The minimum value of $ z = 2x_1 + 3x_2 $ subject to the constraints $ 2x_1 +7x_2\geq 22 $ , $ x_1+x_2\ge6,5x_1+x_2\geq 10 $ and $ x_1 ,x_2 \ge 0 $ is
AMUAMU 2018
Solution:
We have, $z=2 x_{1}+3 x_{2}$ Subject to the constraints
$2 x_{1}+7 x_{2} \geq 22 $
$x_{1}+x_{2} \geq 6 $
$5 x_{1}+x_{2} \geq 10$
$x_{1}, x_{2} \geq 0$
The graph of inequalities are
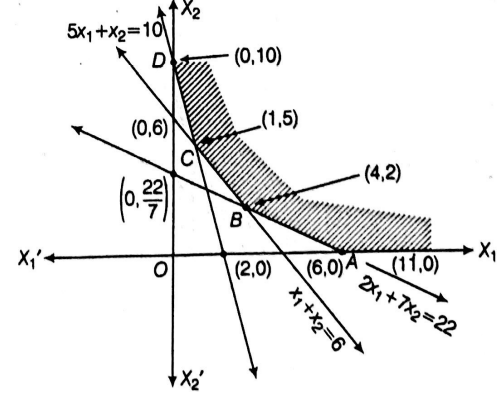
The feasible region are $A B C D$
Corner points
$X = 2x_1 + 3x_2$
A
A (11, 0)
i
22 + 0 = 22
B
B(4, 2 )
ii
8 + 6 = 14
C
C(1, 5)
iii
2 + 15 = 17
D
D ( 0, 10)
iv
0 + 30 = 30
Minimum value of $Z$ ia $14$
| Corner points | $X = 2x_1 + 3x_2$ | ||
|---|---|---|---|
| A | A (11, 0) | i | 22 + 0 = 22 |
| B | B(4, 2 ) | ii | 8 + 6 = 14 |
| C | C(1, 5) | iii | 2 + 15 = 17 |
| D | D ( 0, 10) | iv | 0 + 30 = 30 |