1. Tardigrade
  2. Question
  3. Mathematics
  4. The minimum value of the objective function z = 2x + 10y for linear constraints x ≥ 0, y ≥ 0, x - y ≥ 0 , x - 5y ≤ - 5 , is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

Q. The minimum value of the objective function $z = 2x + 10y$ for linear constraints $x \geq 0, y \geq 0, x - y \geq 0 , x - 5y \leq - 5 $, is

Linear Programming

Solution:

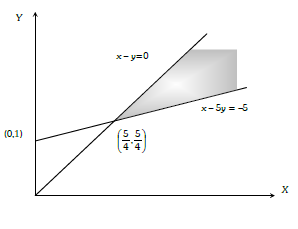
Required region is unbounded whose vertex is $\left( \frac{5}{4} , \frac{5}{4} \right) .$
Hence the minimum value of objective function is
$ = 2 \times \frac{5}{4} + 10 \times \frac{5}{4} = 15 . $

Solution Image