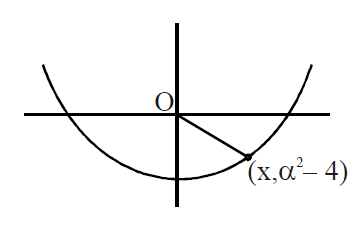Q. The minimum distance of a point on the curve $y = x^2 - 4$ from the origin is :
Solution:
$D=\sqrt{\alpha^{2}+\left(\alpha ^{2}-4\right)^{2}}$
$D^{2}=\alpha ^{2}+\alpha ^{4}+16-8\alpha ^{2}$
$=\alpha ^{4}-7\alpha ^{2}+16$
$\frac{dD^{2}}{d\alpha }=4\alpha ^{3}-14\alpha =0$
$2\alpha \left(2\alpha ^{2}-7\right)=0$
$\alpha ^{2}=\frac{7}{2}$
$D^{2}=\frac{49}{4}-\frac{49}{2}+16 =-\frac{49}{2}+16=\frac{15}{4}$
$D=\frac{\sqrt{15}}{2}$