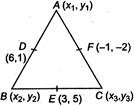
Q. The mid points of the sides of a triangle are $ D(6,1),\,\,E(3,\,5) $ and $ F(-1,-2), $ then the vertex opposite to $D$ is
J & K CETJ & K CET 2007Straight Lines
Solution:
Let the coordinates of A, B, C are
$ ({{x}_{1}},{{y}_{1}}), $
$ ({{x}_{2}}{{y}_{2}}),\,({{x}_{3}}{{y}_{3}}) $
respectively. Given mid points $ D(6,1),\,\,\,\,\,E(3,5) $
and $ F(-1,-2) $ of the sides AB, BC and CA of the triangle.
$ \therefore $ $ \frac{{{x}_{1}}+{{x}_{2}}}{2}=6, $
$ \frac{{{y}_{1}}+{{y}_{2}}}{2}=1 $
$ \Rightarrow $ $ \left. \begin{matrix} {{x}_{1}}+{{x}_{2}}=12, \\ {{y}_{1}}+{{y}_{2}}=2 \\ \end{matrix} \right\} $ ..(i)
Similarly, $ \left. \begin{matrix} {{x}_{2}}+{{x}_{3}}=6, \\ {{y}_{2}}+{{y}_{3}}=10 \\ \end{matrix} \right\} $ ..(ii)
and $ \left. \begin{matrix} {{x}_{1}}+{{x}_{3}}=-2 \\ {{y}_{1}}+{{y}_{3}}=-4 \\ \end{matrix} \right\} $ ..(iii)
On solving Eqs. (i), (ii) and (iii), we get
$ {{x}_{1}}=2,\,{{x}_{2}}=10,\,{{x}_{3}}=-4 $ and $ {{y}_{1}}=-6,\,{{y}_{2}}=8,\,{{y}_{3}}=2 $
Now, the vertex opposite to D is C ie, $ (-4,2) $