Q. The maximum value of $z = 6x + 8y$ subject to $x-y\ge0, x+3y \le 12, x\ge 0, y\ge 0 $ is
MHT CETMHT CET 2019
Solution:
We have, $z=6 x+8 y$
subject to constrants $x-y \geq 0, x+3 y \leq 12, x \geq 0$
$y \geq 0$
On taking given constraints as equations, we get the following graph
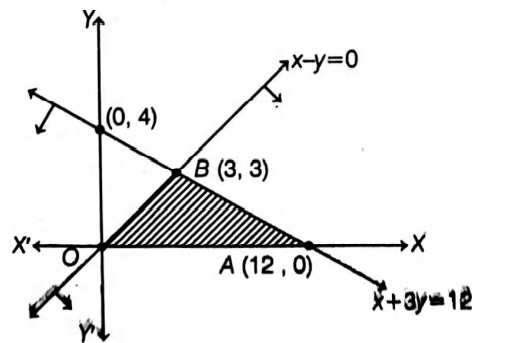
Intersecting point of the line $x-y = 0$ and $x+8 y=12$ is $B (3, 3)$
Here, $OABO$ is the required reasible region
Whose corner points are $O (0, 0), A(12, 0)$ and $B(0 ,4) $ Now,
Comer points
$Z =6x + 8y$
$O(0,0)$
$6 \times 0+8 \times 0=0$
$A(12, 0) $
$6 \times 12+8 \times 0=72$ (maximum)
$B(3, 3)$
$6 \times 3+8 \times 3=42$
| Comer points | $Z =6x + 8y$ | ||
| $O(0,0)$ | $6 \times 0+8 \times 0=0$ | ||
| $A(12, 0) $ | $6 \times 12+8 \times 0=72$ (maximum) | ||
| $B(3, 3)$ | $6 \times 3+8 \times 3=42$ | ||