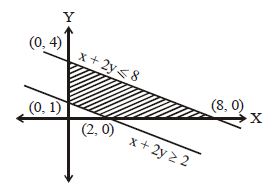
Q. The maximum value of $z = 3x + 2y$ subject to $x + 2y \geq 2, x + 2y \leq 8, x, y \geq 0$ is :
Linear Programming
Solution:
Given : $x + 2y \geq 2 $ .....(1)
$ x + 2y \leq 8$ ......(2)
and $ x,y \geq 0$
For equation (1)
$ \frac{x}{2} + \frac{y}{1} = 1$ and for equation (2)
$ \frac{x}{8} + \frac{y}{4} = 1$
Given : z = 3x+2y
At point $(2, 0); z = 3 \times 2 + 0 = 6$
At point $(0, 1); z = 3 \times 0 + 2 \times 1 = 2$
At point $(8, 0); z = 3 \times 8 + 2 \times 0 = 24 $
At point $(0, 4); z = 3 \times 0 +2 \times 4 = 8$
$\therefore $ maximum value of z is 24 at point $(8, 0)$.