Q. The maximum angular displacement of a simple pendulum of length $l$ is $\theta $ . Find the maximum kinetic energy of a bob of mass $m$ .
NTA AbhyasNTA Abhyas 2020
Solution:
When pendulum passes through mean position, then its kinetic energy will be maximum.
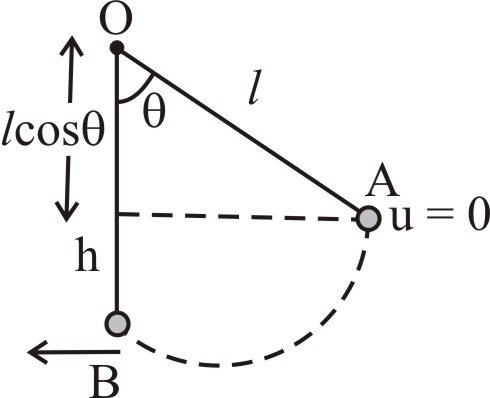
So, by conservation of mechanical energy from A to B
$M.E_{A}=M.E_{B}$
i.e. $mgh=\left(\right.K.E.\left(\left.\right)_{max .}$ ............ (i)
By diagram, $h=l\left(\right.1-cos\theta \left.\right)$ ............ (ii)
By equations (i) and (ii), we get
$\left(\right.K.E.\left(\left.\right)_{max .}=mgl\left(\right.1-cos\theta \left.\right)$

So, by conservation of mechanical energy from A to B
$M.E_{A}=M.E_{B}$
i.e. $mgh=\left(\right.K.E.\left(\left.\right)_{max .}$ ............ (i)
By diagram, $h=l\left(\right.1-cos\theta \left.\right)$ ............ (ii)
By equations (i) and (ii), we get
$\left(\right.K.E.\left(\left.\right)_{max .}=mgl\left(\right.1-cos\theta \left.\right)$