Q. The maximum and minimum values of the objective function z = 3x + 4y subject to the constrains 2x + 3y $\leq$ 6, x + y $\geq$ 1, x $\geq$ 0, y $\geq$ 0, are
Linear Programming
Solution:
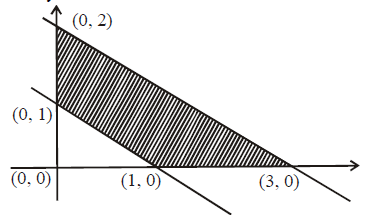
The line 2x + 3y = 6 meets the coordinate axes at (3, 0) and (0, 2). Moreover, for the origin (0, 0), 2x + 3y $\leq$ 6 gives 0 + 0 $\leq$ 6 which is true. Hence the region of feasible solution is on the same side of the line as the origin (0, 0). The line x + y $\geq$ 1 meets the coordinate axes at (1, 0) and (0, 1). Also, for (0, 0), 0 + 0 $\geq$ 1 is false. Hence the region of feasible solution lies on the opposite side of the origin . With x $\geq$ 0, y $\geq$ 0, the feasible region is the shaded one. The vertices are at (1, 0), (3, 0), (0, 2) and (0, 1). At these vertices, the value of the objective function is :
At (1, 0); z = 3 + 0 = 3
at (3, 0) z = 9 + 0 = 9,
at (0, 2) z = 0 + 8 = 8
at (0, 1) z = 0 + 4 = 4.
Hence the maximum value is 9 for x = 3, y= 0 and the minimum value is 3 for x = 1, y = 0.