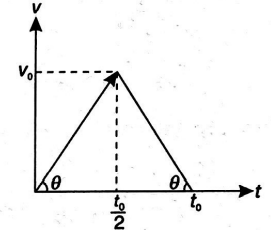
Question

The maximum acceleration or deceleration that a train may have is $a=5\, ms ^{-2}$. The minimum time in which the train may reach from one station to the other separated by a distance $d=500\, m$ is $t_{0}=5\, ns$. The value of $n$ is______.

Answer 1

From the graph,

$d=\frac{1}{2} \times v_{0} t_{0}=\frac{v_{0} t_{0}}{2}$
and $\tan \theta=a=\frac{v_{0}}{t_{0} / 2}=\frac{2 v_{0}}{t_{0}}$
$\therefore v_{0}=\frac{a t_{0}}{2}$
$\therefore d=\frac{t_{0}}{2} \times \frac{a t_{0}}{2}=\frac{a t_{0}^{2}}{4}$
$\therefore t_{0}=2 \sqrt{\frac{d}{a}}=2 \sqrt{\frac{500}{5}}$
$=20\, s =20=5\, n$
$\therefore n=4$