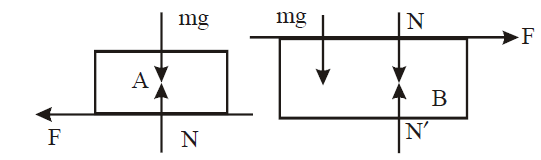
Q.
The masses of blocks $A$ and $B$ are $m$ and $M$ respectively. Between $A$ and $B$, there is a constant frictional force $F$ and $B$ can slide on a smooth horizontal surface. $A$ is set in motion with velocity while $B$ is at rest. What is the distance moved by $A$ relative to $B$ before they move with the same velocity?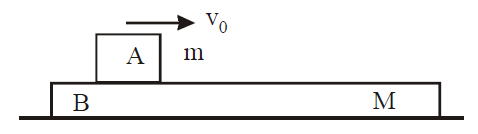
BITSATBITSAT 2015
Solution:
For the blocks $A$ and $B FBD$ as shown below Equations of motion
$a_{A}=\frac{F}{M}$ (in $-x$ direction)
$a_{B}=\frac{F}{M}$ (in $+x$ direction)
Relative acceleration, of $A w . r . t . B$,
$a_{A, B}=a_{A}-a_{B}=-\frac{F}{m}-\frac{F}{M}$
$=-F\left(\frac{M+m}{M m}\right)$
(along $-x$ direction ) Initial relative velocity of $A$ w.r.t $B, u_{A B}=v_{0}$
using equation $v^{2}=u^{2}+2 a s$
$0=v_{0}^{2}-\frac{2 F(m+ M) S}{M m}$
$\Rightarrow S=\frac{M m v_{0}^{2}}{2 F(m+ M)}$
i.e., Distance moved by $A$ relative to $B$
$S_{A B}=\frac{M m v_{0}^{2}}{2 F(m+ M)}$