Q.
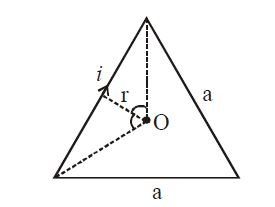
The magnitude of the magnetic field at the center of an equilateral triangular loop of side $1\,m$ which is carrying a current of $10\, A$ is :
[Take $\mu_0 = 4\pi \times 10^{-7} \; NA^{-2}]$
Solution:
The magnetic field at the center of an equilateral triangular loop will be given as
B=$B = 3 \left[\frac{\mu_{0}i}{4\pi r} \left(\sin60^{\circ}+ \sin60^{\circ}\right)\right] $
Here, $r= \frac{a}{2\sqrt{3}} = \frac{1}{2\sqrt{3}} $
$ B= 3 \left[\frac{4\pi\times10^{7}\times 10\times 2\sqrt{3} }{4 \pi\times 1} \left[\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2}\right]\right] $
$B = 18 \times10^{-6} = 18\, \mu T $