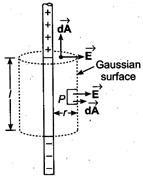
Question

The magnitude of electric field at distance $ r$ from an infinitely thin rod having a linear charge density $ \lambda , $ is (use Gauss's law)

• A. $E=\frac{\lambda}{2 \pi \varepsilon_{0} r}$
• B. $E=\frac{2 \lambda}{\pi \varepsilon_{0} r}$
• C. $E=\frac{2 \lambda}{4 \pi \varepsilon_{0} r}$
• D. $E=\frac{4 \lambda}{\pi \varepsilon_{0} r}$

Answer 1

Answer: (A)

Gauss theorem states that the total electric flux $(\phi)$ through any closed surface is equal to $\frac{1}{\varepsilon_{0}}$ times the 'net' charge $q$ enclosed by the surface.
$\phi_{z}=\int \vec{E} \cdot \overrightarrow{d A}=\frac{Q}{\varepsilon_{0}}$
Taking cylindrical Gaussian surface of radius $r$, height h curved surface $=2 \pi r h$.
Electric flux through it $=E \times 2 \pi r h$
Charge enclosed $=\lambda h$
$\therefore $ From Gauss theorem,
Charge $=\varepsilon_{0} \times$ (Electric flux)
$\Rightarrow \varepsilon_{0} E \times 2 \pi r h=\lambda h$
$\Rightarrow E=\frac{1}{2 \pi \varepsilon_{0}} \cdot \frac{\lambda}{r}=\frac{\lambda}{2 \pi \varepsilon_{0} r}$