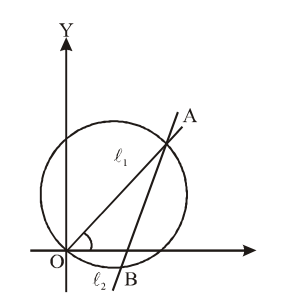
Question

The locus of the mid point of all chords of the circle $x^{2}+y^{2}-2 x-2 y=0$ such that the pair of lines joining $(0,0) \&$ the point of intersection of the chords with the circles make equal angle with axis of $x$, is

• A. $x-y=2$
• B. $x+y=2$
• C. $x+y=-2$
• D. None of these

Answer 1

Answer: (B)

Let mid-point $ \equiv(h, k) $
$ \therefore h^{2}+k^{2}-2 h-2 k=h x+k y-(x+h)-(y+k)$
$ \Rightarrow h^{2}+k^{2}-h-k=h x+k y-x-y $
$\Rightarrow \frac{(h-1) x+(k-1) y}{h^{2}+k^{2}-h-k}=1 $
Homogenization
$ x^{2}+y^{2}-2 x\left(\frac{(h-1) x+(k-1) y}{h^{2}+k^{2}-h-k}\right)$
$ -2 y\left(\frac{(h-1) x+(k-1) y}{h^{2}+k^{2}-h-k}\right)=0 $
$\therefore \frac{-2(k-1)-2(h-1)}{h^{2}+k^{2}-h-k}=0 $
$\Rightarrow -2 k+2-2 h+2=0 $
$\Rightarrow h+k=2$
$ \therefore $ required locus :
$x+y=2$