Question

The lines $x + y = | a |$ and $ax - y = 1$ intersect each other in the first quadrant. Then the set of all possible values of $a$ is the interval :

• A. $\left(0, \infty\right)$
• B. $[1, \infty)$
• C. $\left(-1, \infty\right)$
• D. $(-1, 1]$

Answer 1

Answer: (B)

$x + y = |a|$
$ax - y = 1$
if $a > 0$
$x + y = a$
$ax - y = 1$
$x\left(1 + a\right) = 1 + a \,as\, x = 1$
$y = a - 1$
It is first quadrant
so $a-1 \ge 0$
$a \ge 1$
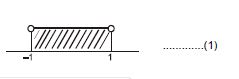
$a \in [1, \infty)$
If $a < 0$
$x + y = - a$
$ax - y = 1$
$+$
$x\left(1 + a\right) = 1 - a$
$x = \frac{1-a}{1+a} > 0 \Rightarrow \frac{a-1}{a+1}< 0$
$y = - a-\frac{1-a}{1+a} $
$= \frac{-a-a^{2}-1+a}{1+a}> 0$
$-\left(\frac{a^{2}+1}{a+1}\right)> 0\quad\Rightarrow \quad \frac{a^{2}+1}{a+1} < 0$
from $\left(1\right)$ and $\left(2\right) a \in \left\{\phi\right\}$
So correct answer is a $[\in 1, \infty)$