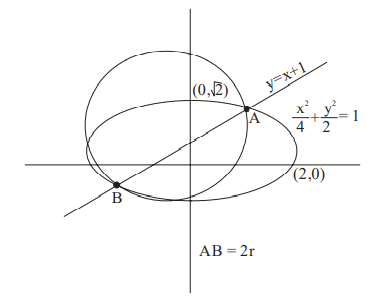
Q. The line $y = x +1$ meets the ellipse $\frac{ x ^{2}}{4}+\frac{ y ^{2}}{2}=1$ at two points $P$ and $Q$. If $r$ is the radius of the circle with $PQ$ as diameter then $(3 r )^{2}$ is equal to
Solution:
Ellipse $x^{2}+2 y^{2}=4$
Line $y=x+1$
Point of intersection
$x^{2}+2(x+1)^{2}=4$
$3 x^{2}+4 x-2=0$
$\left|x_{1}-x_{2}\right|=\frac{\sqrt{40}}{3}$
$A B=2 r=\left|x_{1}-x_{2}\right| \sqrt{1+m^{2}}$
$m$ is slope of given line
$AB =\frac{\sqrt{40}}{3} \sqrt{1+1}$
$2 r=\frac{\sqrt{80}}{3}$
$\Rightarrow r=\frac{\sqrt{80}}{6}$
$(3 r)^{2}=\left(3 \times \frac{\sqrt{80}}{6}\right)^{2}$
$=\frac{80}{4}=20$