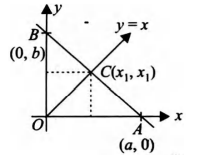
Question

The line $\frac{x}{a} + \frac{y}{b} = 1$ meets the $x$-axis at $A$, the $y$-axis at $B$, and the line $y = x$ at $C$ such that the area of $\Delta AOC$ is twice the area of $\Delta BOC$. Then the coordinates of $C$ are

• A. $\left(\frac{b}{3}, \frac{b}{3}\right)$
• B. $\left(\frac{2a}{3}, \frac{2a}{3}\right)$
• C. $\left(\frac{2b}{3}, \frac{2b}{3}\right)$
• D. none of these

Answer 1

Answer: (C)

Given $ar \Delta AOC = 2(ar\Delta BOC)$
or $\frac{1}{2} (OA)(x_1) = \frac{2\times 1}{2} (OB)(x_1)$
or $ a = 2b$
The equation of $AB$ is
$\frac{x}{a} + \frac{y}{b} = 1 \,....(i)$
or $\frac{x}{2b} + \frac{y}{b} = 1\,....(ii)$
Since point $C$ lies on line $(ii)$, we have
$\frac{x_1}{2b} + \frac{x_1}{b} = 1$
or $x_1 = \frac{2b}{3} = \frac{a}{3}$
or $C \equiv ( \frac{2b}{3}, \frac{2b}{3})$