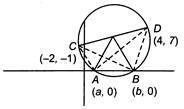
Q. The line segment joining the points (4, 7) and $ (-2,-1) $ is a diameter of a circle. If the circle intersects the x-axis at A and B, then AB is equal to
KEAMKEAM 2010
Solution:
$ \because $ (4, 7) and $ (-2,-1) $ are end points of circle.
$ \Rightarrow $ Centre of circle
$=\left( \frac{4-2}{2},\frac{7-1}{2} \right)=(1,3) $
$ \therefore $ Slope of $ AC=\frac{-1-0}{-2-a}=-\frac{1}{2+a} $ and slope of $ AD=\frac{7-0}{4-a}=\frac{7}{4-a} $
Since, $ \Delta CAD $ is right angle as CD is diameter.
$ \Rightarrow $ (slope of AC (slope of AD)
$=-1 $
$ \Rightarrow $ $ \left( \frac{1}{2+a} \right)\left( \frac{7}{4-a} \right)=-1 $
$ \Rightarrow $ $ \frac{7}{-{{a}^{2}}+2a+8}=-1 $
$ \Rightarrow $ $ {{a}^{2}}-2a-15=0 $
$ \Rightarrow $ $ a=-3,5 $ Similarly, $ b=-3,5 $
$ \therefore $ Point $ A=(-3,0) $ and point $ B=(5,0) $
$ \therefore $ $ AB=\sqrt{{{(-3-5)}^{2}}+{{(0-0)}^{2}}} $
$=\sqrt{{{(-8)}^{2}}}=8 $