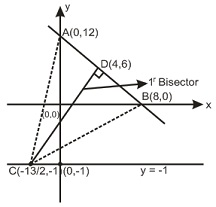
Question

The line $3x+2y=24$ meets $x$ - axis at $B$ and the $y$ - axis at $A$ . The perpendicular bisector of $AB$ meets the line through $\left(\right.0,-1\left.\right)$ parallel to $x$ -axis at $C$ , then the area of the triangle $ABC$ is _____

Answer 1

Equation of $CD$ $\Rightarrow $
$2 \text{x} - 3 \text{y} = \lambda $ .....(1)
It passes through $\left(\right.4,6\left.\right)$ then $\lambda = - 1 0$
$2 \text{x} - 3 \text{y} + 1 0 = 0$ ....(2)
Co-ordinate of $\text{C } \left(- \frac{1 3}{2} \text{,} - 1\right)$
Now the area of triangle
$\Delta = \frac{1}{2} \begin{vmatrix} 0 & 12 & 1 \\ 8 & 0 & 1 \\ -\frac{1 3}{2} & -1 & 1 \end{vmatrix}$
$=\frac{1}{2}\left[\left|0 - 12 \left(8 + \frac{13}{2}\right) + 1 \left(- 8\right)\right|\right]$
$=\frac{1}{2}\left[\left|- 6 \left(29\right) - 8\right|\right]=91$