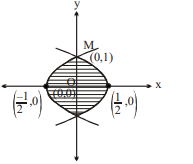
Question

The length of sub-normal at any point $P ( x , y )$ on the curve, which is passing through $M (0,1)$ is unity. The area bounded by the curves satisfying this condition is equal to

• A. $\frac{1}{3}$
• B. $\frac{2}{3}$
• C. $ \frac{4}{3}$
• D. $\frac{8}{3}$

Answer 1

Answer: (C)

We have $\left|\frac{ ydy }{ dx }\right|=1 \Rightarrow \int ydy =\int \pm dx \Rightarrow \frac{ y ^2}{2}= \pm x + C$ But $M (0,1)$ satisfy it, so $C =\frac{1}{2}$
$\Rightarrow y^2= \pm 2 x +1$
Let $C_1: y^2=2\left(x+\frac{1}{2}\right)$ and $C_2: y^2=-2\left(x-\frac{1}{2}\right)$
Clearly required area $=4 \int\limits_{\frac{-1}{2}}^0 \sqrt{2 x +1} dx =\frac{4}{3}$ (square units)