Q. The length of focal chord which makes an angle $ \alpha $ with the axis. of the parabola $ {{y}^{2}}=4ax $ is
JamiaJamia 2010
Solution:
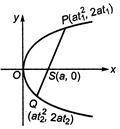
Let $ p(at_{1}^{2},2a{{t}_{1}}) $ and $ Q(at_{2}^{2},2a{{t}_{2}}) $ be the end points of the focal chord PQ of the parabola $ {{y}^{2}}=4ax $ and which makes an angle $ \alpha $ with the axis of parabola.
Now, $ PQ=\sqrt{{{(at_{2}^{2}-at_{1}^{2})}^{2}}+{{(2a{{t}_{2}}-2a{{t}_{1}})}^{2}}} $ $ =a\sqrt{{{(t_{2}^{2}-t_{1}^{2})}^{2}}+4{{({{t}_{2}}-{{t}_{1}})}^{2}}} $ $ =a\sqrt{{{({{t}_{2}}+{{t}_{1}})}^{2}}{{({{t}_{2}}-{{t}_{1}})}^{2}}+4{{({{t}_{2}}-{{t}_{1}})}^{2}}} $ $ =a({{t}_{2}}-{{t}_{1}})\sqrt{t_{2}^{2}+t_{1}^{2}+2{{t}_{1}}{{t}_{2}}+4} $ $ =a({{t}_{2}}-{{t}_{1}})\sqrt{t_{2}^{2}+t_{1}^{2}-2+4} $ $ (\because {{t}_{1}}{{t}_{2}}=-1) $ $ =a({{t}_{2}}-{{t}_{1}})\sqrt{t_{2}^{2}+t_{1}^{2}+2} $ $ =a({{t}_{2}}-{{t}_{1}})\sqrt{(t_{2}^{2}+t_{1}^{2}-2{{t}_{1}}{{t}_{2}})} $ $ (\because {{t}_{1}}{{t}_{2}}=-1) $ $ PQ=a({{t}_{2}}-{{t}_{1}})\sqrt{{{({{t}_{2}}-{{t}_{1}})}^{2}}} $ $ =a{{({{t}_{2}}-{{t}_{1}})}^{2}} $ and slope of $ PQ=\frac{2a{{t}_{2}}-2a{{t}_{1}}}{at_{2}^{2}-at_{1}^{2}} $ $ \tan \alpha =\frac{2a({{t}_{2}}-{{t}_{1}})}{a({{t}_{2}}-{{t}_{1}})({{t}_{2}}-{{t}_{1}})} $ $ \Rightarrow $ $ \tan \alpha =\frac{2}{{{t}_{1}}+{{t}_{2}}} $ $ \Rightarrow $ $ 2\cot \alpha ={{t}_{1}}+{{t}_{2}} $ Again, we have Eq. (i) $ PQ=a{{({{t}_{2}}-{{t}_{1}})}^{2}} $ $ =a[{{({{t}_{2}}+{{t}_{1}})}^{2}}-4{{t}_{1}}{{t}_{2}}] $ $ =a[{{(2\cot \alpha )}^{2}}+4] $ $ [\because {{t}_{1}}+{{t}_{2}}=2\cot \alpha \,\,and\,{{t}_{1}}{{t}_{2}}=-1] $ $ =4a(1+{{\cot }^{2}}\alpha ) $ $ PQ=4a\,\cos e{{c}^{2}}\alpha $