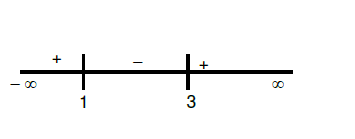Q. The interval in which the function $f(x) = x^3 - 6x^2 + 9x + 10$ is increasing in
Solution:
$f\left(x\right)=x^{3}-6x^{2}+9x+10$
$f '\left(x\right)=3x^{2}-12x+9$
$f '\left(x\right)=0$
$3x^{2}-12x+9=0 \quad$(dividing by $3$)
$x^{2}-4x+3=0$
$x^{2}-3x-x+3=0$
$x\left(x-3\right)-1\left(x-3\right)=0$
$x=3, 1$
$(-\infty, 1 ] \cup[3,\infty)$