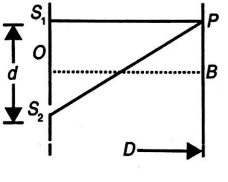
Q. The intensity at the maximum in a Young's double slit experiment is $I_{0}$. Distance between two slits is $d=5 \lambda$, where $\lambda$ is the wavelength of light used in the experiment. The intensity infront of one of the slits on the screen placed at a distance $D=10 d$ is $\frac{I_{0}}{n}$. Find $n$.
Wave Optics
Solution:
Path difference $=S_{2} P-S_{1} P$
$=\sqrt{D^{2}+d^{2}}-D$
$=D\left(1+\frac{1}{2} \frac{d^{2}}{D^{2}}\right)-D$
$=D\left[1+\frac{d^{2}}{2 D^{2}}-1\right]=\frac{d^{2}}{2 D}$
$\Delta x=\frac{d^{2}}{2 \times 10 d}=\frac{d}{20}=\frac{5 \lambda}{20}=\frac{\lambda}{4}$
$\Delta \phi=\frac{2 \pi}{\lambda} \cdot \frac{\lambda}{4}=\frac{\pi}{2}$
So, intensity at the desired point is
$I=I_{0} \cos ^{2} \frac{\phi}{2}=I_{0} \cos ^{2} \frac{\pi}{4}=\frac{I_{0}}{2}$