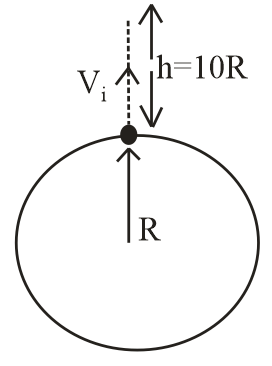
Question

The initial velocity $v_{i}$ required to project a body vertically upward from the surface of the earth to reach a height of $10R,$ where $R$ is the radius of the earth, may be described in terms of escape velocity $v_{e}$ such that $v_{i}=\sqrt{\frac{x}{y}}\times v_{e}.$ The value of $x$ will be

Answer 1

Here $R=$ radius of the earth
From energy conservation
$\frac{- Gm_{e} m}{R}+\frac{1}{2}mv_{i}^{2}=\frac{- Gm_{e} m}{11 R}+0$
$\frac{1}{2}mv_{i}^{2}=\frac{10}{11}\frac{Gm_{e} m}{R}$
$V_{i}=\sqrt{\frac{20}{11} \frac{Gm_{e}}{R}}$
$V _{ i }=\sqrt{\frac{10}{11}} v _{ e }\left\{\because \quad\right.$ escape velocity $\left.v_{e}=\sqrt{\frac{2 Gm _{e}}{ R }}\right\}$
Then the value of $x=10$