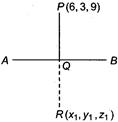
Q. The image of the point $ (6,3,9) $ in the straight line $ x-2=\frac{1-y}{2}=\frac{z}{2} $ is
J & K CETJ & K CET 2009Three Dimensional Geometry
Solution:
Given equation of line is
$ \frac{x-2}{1}=\frac{y-1}{-2}=\frac{z-0}{2}=k $ [say]
Any point on the line is $ Q(k+2,\,\,-2k+1,2k) $
Direction ratios of PQ are
$ (k+2-6,-2k+1-3,2k-9) $ ie, $ (k-4,\,-2k-2,\,2k-9), $
Since, the line $ PQ $ is perpendicular to $ AB $ .
$ \therefore $ $ 1(k-4)-2(-2k-2)+2(2k-9)=0 $
$ \Rightarrow $ $ k-4+4k+4+4k-18=0 $
$ \Rightarrow $ $ 9\,k=18 $
$ \Rightarrow $ $ k=2 $
$ \therefore $ Point Q is $ (4,-3,4) $ .
Let the image of P about line AB is
$ R({{x}_{1}},{{y}_{1}},{{z}_{1}}), $
Where Q is the mid point of PR.
$ \therefore $ $ \frac{{{x}_{1}}+6}{2}=4,\,\frac{{{y}_{1}}+3}{2}=-3,\,\frac{{{z}_{1}}+9}{2}=4 $
$ \Rightarrow $ $ {{x}_{1}}=2,\,{{y}_{1}}=-9,\,{{z}_{1}}=-1 $