Question

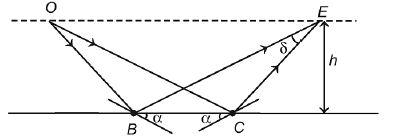
The image of an object $O$ due to reflection from the surface of a lake is elongated due to the ripple s on the water surface caused by a light breeze. This is because the ripples act as tilted mirrors as shown below. Consider the case, where $O$ and the observer $E$ are at the same height above the surface of the lake. If the maximum angle that the ripples make with the horizontal is a , the $n$ the angular extent $\delta$ of the image will be

• A. $\frac{\alpha }{2}\:$
• B. $\alpha \:$
• C. $2\alpha \:$
• D. $4\alpha \:$

Answer 1

Answer: (C)

We can consider ripples as plane mirrors reflecting light to form image with angular extent $\delta$.
It is given $O$ and $E$ are at same level, so $O E B C$ is a trapezium with $O E || B C$.
Now, different angles of trapezium $O E B C$ are as shown below.

$ \angle 1 =90^{\circ}-\beta-\alpha $
$ \angle 2 =90^{\circ}-\gamma-\alpha$
$ \angle O P B =\angle E P C $ and $ \angle O P E =\angle B O C $
$ \Rightarrow 90^{\circ}-\beta-\alpha =90^{\circ}-\gamma-\alpha$
$ \Rightarrow \beta =\gamma $ ...(i)
As , $ \angle O P C =180^{\circ}$
$ \Rightarrow 180^{\circ} =\beta+\gamma+2 \alpha+180-2 \gamma-\delta$
$\Rightarrow 2 \alpha+\beta-\gamma-\delta=0 $
$ \Rightarrow \delta=2 \alpha [\because \beta=r $ from Eq. (i)$]$