Question

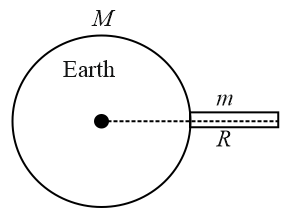
The gravitational force between earth of radius $R$ and mass $M$ and rod of length $R$ and mass $m$ placed as shown in the figure is $\frac{12 G M m}{n R^{2}}$ . Find the value of $n$ .

Answer 1

Net force on the rod is equal to centripetal force.
Here, mass of small element at distance $x$ is $dm=\frac{m}{R}dx$
So, gravitational force, $dF_{g}=\frac{G M d m}{\left(R + x\right)^{2}}=\frac{G M m d x}{R \left(R + x\right)^{2}}$
$dF_{g}=\frac{G M m}{\left( R + x \right)^{2} R}dx$

$=\frac{G M m}{R}\int\limits _{0}^{R} \frac{d x}{\left( R + x \right)^{2}}$
$F_{g}=\frac{G M m}{2 R^{2}}$
$F_{g}=\frac{12 G M m}{24 R^{2}}$
Hence, $n=24$ .