Q.
The gravitational force acting on a particle, due to a solid sphere of uniform density and radius $R$, at a distance of $3\, R$ from the centre of the sphere is $F_{1}$. A spherical hole of radius $(R / 2)$ is now made in the sphere as shown in the figure. The sphere with hole now exerts a force $F_{2}$ on the same particle. Ratio of $F_{1}$ and $F_{2}$ is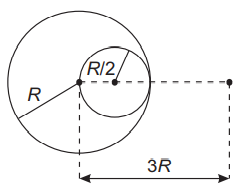
EAMCETEAMCET 2013
Solution:
