Question

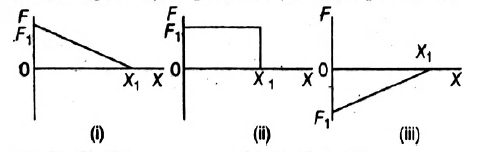
The graphs below show the magnitude of the force on a particle as it moves along the positive $ X $ -axis from the origin to $ X - X_{1} $ . The force is parallel to the $ X $ -axis and conservative. The maximum magnitude $ F_{1} $ has the same value for all graphs. Rank the situations according to the change in the potential energy associated with the force, least (or most negative) to greatest (or most positive).

• A. (i), (ii), (iii)
• B. (i) (iii), (ii),
• C. (iii), (ii), (i)
• D. (ii), (i), (iii)

Answer 1

Answer: (D)

As we know, for a conservative force field
$dU=-F_{con} dr$
where, $dU$ = change in potential energy,
$F_{con}$= conservative force (or $F_{in}$)
and $dr$ = change in position of the particle
$dU =-F_{in} dr$ or $\Delta U=-\int\limits_{r_1}^{r_{2}} F_{in} dr $
$U_{2}-U_{1}=-\int\limits_{r_1}^{r_{2}} F_{in} dr$ =-work done by $F_{in}$ (or $W_{in})$
For graph $\left(i\right)$, $W_{in}=\frac{F_{1}\cdot x_{1}}{2}$
For graph $\left(ii\right)$, $W_{in}=F_{1}\cdot x_{1}$
and for graph $\left(iii\right)$, $W_{in}=\frac{-F_{1}\cdot x_{1}}{2}$
Thus, change in potential energy
For graph $\left(i\right)$, $\Delta U_{1}=\frac{-F_{1}x_{1}}{2}$ graph $\left(ii\right)$ $\Delta U_{2}=-F_{1}x_{1}$
graph, $\left(iii\right)$ $\Delta U_{3}=\frac{F_{1}x_{1}}{2}$
Thus, we have,
$\Delta U_{2} < \, \Delta U_{1}<\, \Delta U_{3}$ (according to the question)
or $(ii) <\, (i) <\, (iii)$